Polymers are viscoelastic and therefore are interesting for damping applications, especially when used at temperatures laying in their glassy-to-rubbery transition where the material is showing significant viscoelasticity. During his PhD co-advised by Gregoire Allaire, Samuel Amstutz and me, Antoni Joubert has worked on the shape optimization of thin structures such as beams and plates to enhance their damping properties when submitted to free vibrations. He has used several constitutive equations, from the plate Kirchoff-Love and Reissner-Mindlin models to the bulk 3D linear viscoelastic model to reach the best structures. Several interesting results were obtained:
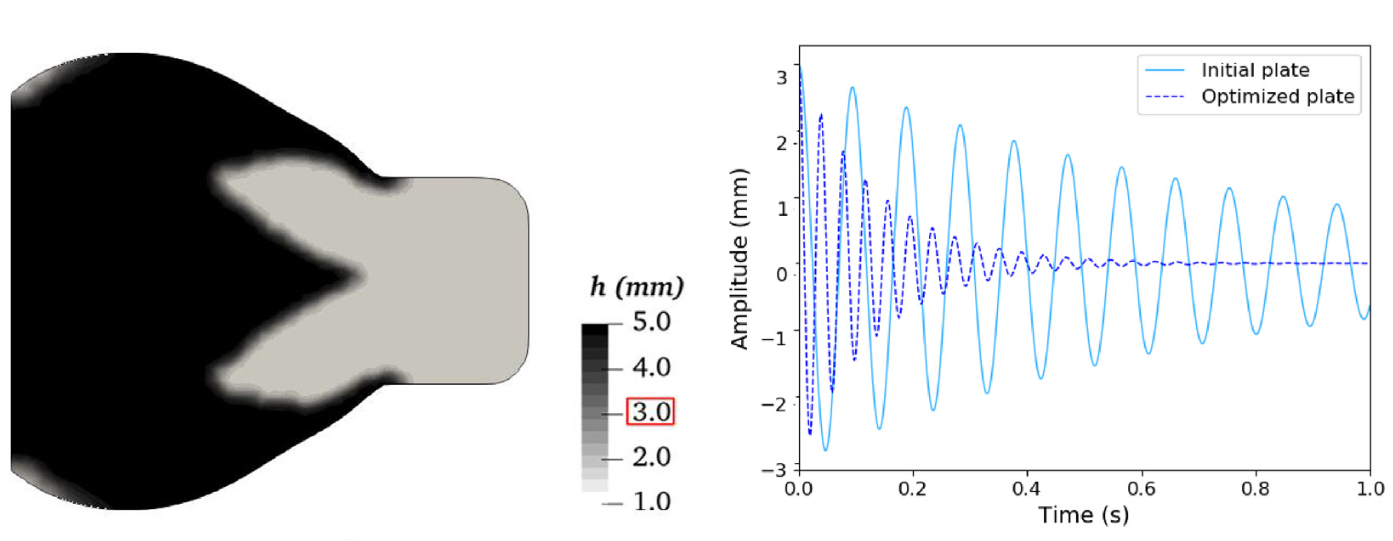
For a given set of material parameters, tremendous damping enhancement may be achieved by shape optimization. Figure 1 shows the free vibrations for a rectangular cantilever plate of constant thickness and the shape optimized plate having the same amount of material.
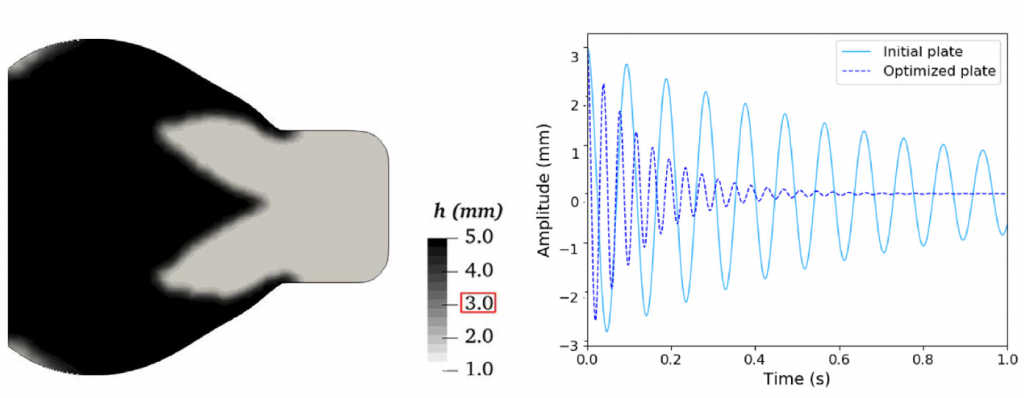
Figure 1. Shape and thickness profiles of the optimized cantilever plate, and comparison between the free vibrations of the optimized cantilever plate and a rectangular plate of constant thickness.
Taking into account the actual viscoelasticity of the Poisson’s ratio demands a lot of theoretical and computational efforts without necessarily changing significantly the final design of the structures.
2D topology optimizations have conducted to design with undesired weakness points (Figure 2).

Figure 2. Topology optimization of a 2D cantilever plate submitted to free vibration revealing structural weakness.
The latter result is classic for topology optimization of linear elastic structure too. When considering a 3D structure, small cantilevers within the structure provide with a more satisfactory design for actual applications (Figure 3).
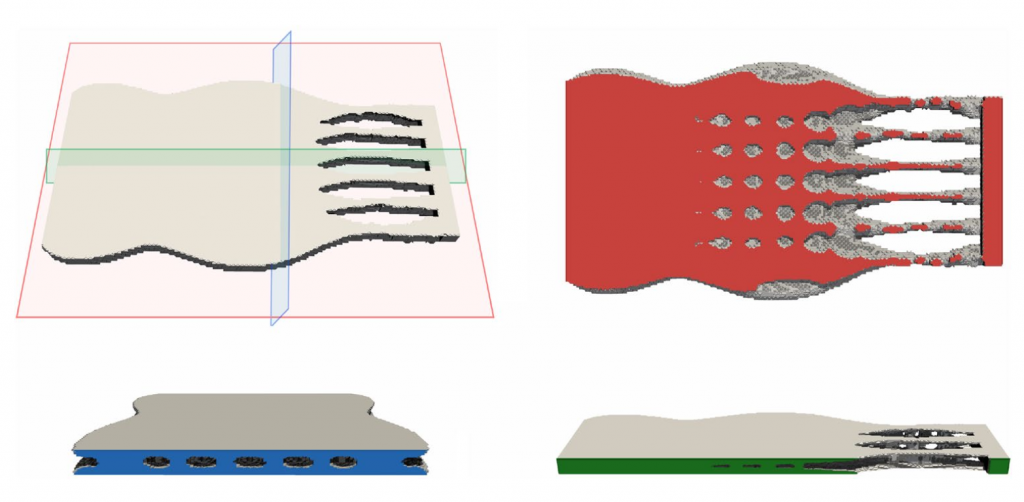
Figure 3. 3D optimized structure showing cantilever aligned in the thickness direction that reinforces the structure.
Details on this work may be found here:
A. Joubert, G. Allaire, S. Amstutz, J. Diani. Damping optimization of viscoelastic cantilever beams and plates under free vibrations. Computer and Structures (2022), 268,106811.
A. Joubert, G. Allaire, S. Amstutz, J. Diani. Damping optimization of thin structures, application and analysis. Structural and multidisciplinary optimization (2023), 66, 149.
This work was supported by the Chair “Modeling advanced polymers for innovative material solutions” led by École Polytechnique (l’X) and the Fondation de l’École Polytechnique and sponsored by Arkema.